La fisica del biliardo (subatomica)
Posted: Luglio 27th, 2008 | Author: packz | Filed under: Fisica spicciola | Commenti disabilitati su La fisica del biliardo (subatomica)Sappiamo tutti cosa sia una collisione, cioé un urto fra due o più oggetti che eventualmente può avere una conseguenza emotiva o legale; tuttavia rimanendo nell’ambito della fisica spicciola e sopratutto nel caso semplice della collisione fra due semplici corpi di massa e velocità predeterminate esistono delle semplici leggi di conservazione che ci permettono di studiare il risultato di tali urti. Nel caso di urto elastico (cioé di un urto in cui l’energia non viene dispersa per attriti, deformazione etc…) le leggi vigenti sono quelle della conservazione dell’energia e dell’impulso rappresentate dalle formule seguenti
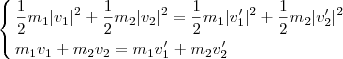
Se prendiamo in esame gli urti che si verificano nel gioco del biliardo, dove tutte le palle hanno la stessa massa e dove la pallina da colpire risulta ferma si hanno le seguenti condizioni
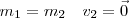
rappresentate dal seguente grafico
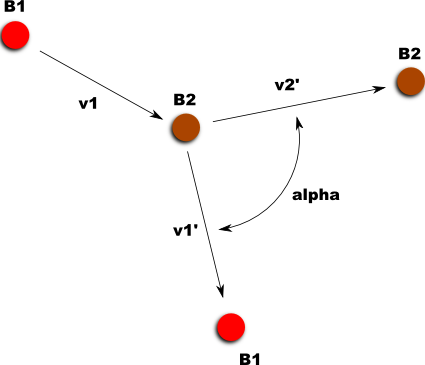
Le condizioni dell’urto possono essere sostituite all’interno delle formule della conservazione dell’energia in maniera da ottenere la seguente relazione fra i moduli della velocità entrante e uscente
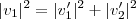
Se immaginate di mettere questi tre vettori idealmente uno dopo l’altro formereste un triangolo, quindi la formula appena scritta ci dice che la somma dei quadrati costruiti sui cateti è uguale al quadrato costruito sull’ipotenusa: l’angolo di separazione fra le direzioni dei due corpi dopo l’urto è un angolo retto!!! Attenzione però che non è detto che esista un angolo di separazione: se noi colpiamo in maniera perfettamente frontale la palla da 8 non esiste nessuna direzione preferenziale che la natura possa scegliere e quindi il sistema totale si deve muovere ancora lunga la stessa direzione della velocità di entrata del primo corpo; ovviamente non si può più formare un triangolo rettangolo e l’unica scelta è quella in cui le velocità vengano scambiate
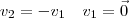
cioé la pallina ferma si muove con la stessa velocità di quella che la ha colpita mentre quest’ultima rimane ferma al suo posto (come potete sperimentare empiricamente quando giocate a biliardo). Nel titolo c’era anche la dicitura "subatomica", bene questo è dovuto al fatto che questo semplice meccanismo di urto e conservazione può essere applicato anche nella fisica subatomica, cambiando alcune formule per rispecchiare legami esoterici fra energia e momento in particelle a massa nulla
Prima di tutto le due leggi di conservazione possono essere riassunte in una sola, la legge di conservazione del quadri-impulso (nella fisica moderna il tempo viene visto come una coordinata qualsiasi portando a quattro il numero di quantità di moto e di posizione da conoscere per identificare correttamente lo stato del sistema); il quadrimpulso può essere scritto nel seguente modo
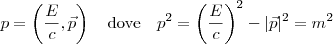
per le particelle con massa a riposo m, mentre per le particelle senza massa, quale per esempio il fotone, la relazione risulta essere la seguente
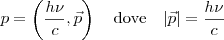
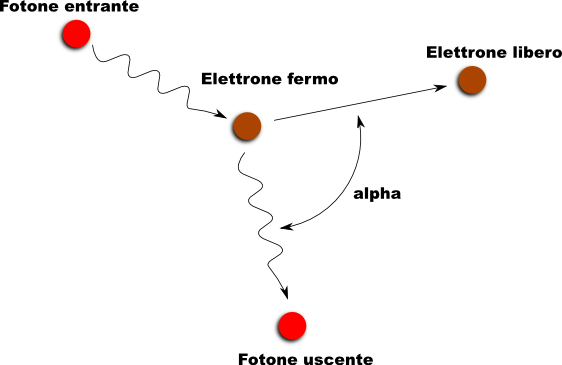
Se consideriamo un elettrone all’interno di un orbitale atomico che entra in interazione con un fotone di frequenza nu possiamo considerare l’elettrone fermo e vedere in maniera totalmente analoga l’urto come quello descritto sopra tra palle da biliardo, tenendo ovviamente conto della diversa forma delle quantità fisiche in gioco; la formula finale (la cui derivazione lascio a wikipedia)
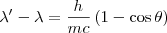
lega la differenza fra lunghezza d’onda del fotone uscente e quello incidente con l’angolo di diffusione. Questa relazione ha una importanza fondamentale in quanto permette di riconoscere alla radiazione luminosa (qui rappresentata dal fotone) proprietà proprie delle particelle; questo particolare effetto viene chiamato Compton dal nome del primo scienziato che studiò ed elaborò la formula subito sopra, usando la teoria della radiazione di Einstein (in cui si affermava che la luce era composta da quanti aventi energia direttamente proporzionale alla propria frequenza) allora ancora in forse.Altri esperimenti simili vennero in seguito, volti alla dimostrazione contraria che gli elettroni si comportano come onde: in particolare George Thomson usò delle lastre di celluloide mostrando delle frange di interferenza prodotto da gli elettroni che interagivano con essa; questo avvenne 28 anni dopo che suo padre J.J Thomson scoprì l’elettrone come particella. Benchè entrambi trovarono risultati opposti entrambi avevano ragione e furono insigniti del premio Nobel.
APPENDICE: Punto di contatto
Tornando alla trattazione dell’urto di corpi materiali in maniera elastica, si lascia un’ambiguità per quanto riguarda l’effettiva direzione che le palline percorrono dopo l’urto siccome abbiamo detto che (quando hanno masse uguali e una delle due è ferma) le loro direzioni formano un angolo di 90 gradi, ma potete immaginare che questa relazione è verificata anche per un urto in cui i due corpi tornano indietro!!! Per capire quale direzione viene effettivamente presa, basta considerare il seguente schema
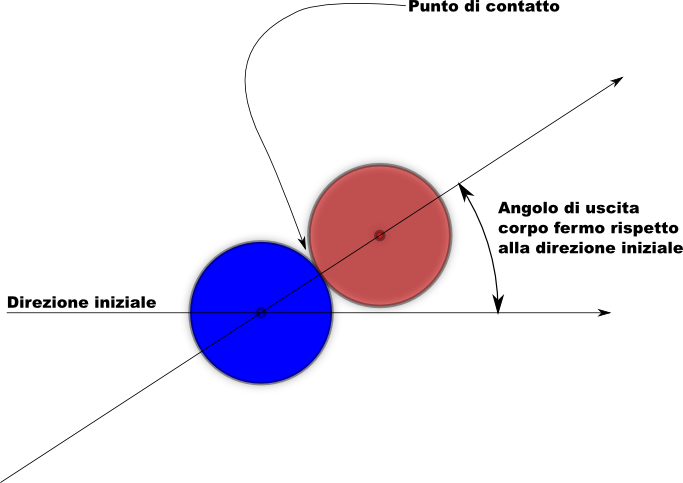
la forza che il primo corpo imprime sul secondo è diretta lungo la congiungente dei due centri di massa (ipotizzo corpi sferici con densità omogenea) e quindi il suo cambio di velocità sarà in tale direzione; è facile immaginare che siccome il corpo è fermo la sua nuova direzione sia proprio quella. Se pensate a questo problema dal punto di vista geometrico, esistono soltanto due direzioni che questo sistema genera
- La direzione del moto della pallina iniziale (che coincide con il moto del centro di massa del sistema)
- La direzione formata dai due centri di massa al momento del contatto
e quindi sono le uniche due direzioni che per simmetria possono rientrare nella soluzione e non sicuramente la direzione formata fra il cervello di Bruno Vespa e la figa di Mara Carfagna. Il caso limite è quando queste direzioni coincidono, caso in cui ovviamente l’unica possibilità è che la direzione venga preservata (se una delle due sfilasse da un lato vorrebbe dire che Dio ha scelto una direzione preferenziale, questo va bene per i neutrini, ma non per le palle da biliardo).
Questo modo di studiare i problemi permette in alcuni casi di poter affermare il comportamento di certi sistemi semplicemente osservando le loro caratteristiche come per esempio è possibile trovare la formula che lega il periodo del pendolo alle sue caratteristiche geometriche semplicemente tenendo conto delle unità di misura.