Posted: Giugno 7th, 2009 | Author: packz | Filed under: Approfondimenti, Math | Commenti disabilitati su Monty Hall problem
Supponiamo che siate ad un gioco a premi, supponiamo che questo gioco si debba decidere una scatola fra un insieme di tre e che solo una scatola contiene un premio; però il gioco non finisce qui, una volta scelta una scatola, il conduttore del gioco elimina una scatola in cui sicuramente non c’è il premio. A questo punto vi viene chiesto di scegliere se volete cambiare la scatola scelta da voi con quella rimasta e voi ovviamente la cambierete! perchè? semplice, è tutta una questione di probabilità.
Le probabilità si calcolano rapportando i casi favorevoli all’evento di cui vogliamo calcolare la probabilità e tutti i casi possibili: in questo caso vogliamo calcolare la probabilità che una volta scelta una scatola e scambiandola con quella rimasta, io vinca; il numero di casi possibili sono 3, mentre i casi in cui io vinca sono 2, cioè i casi in cui non abbia scelto la scatola in cui c’era effettivamente il premio (cioè avere più culo all’inizio è il caso più sfortunato ;-)).
Detto così effettivamente è meno controintuitivo (dopo un giorno di cazzeggiamenti cerebrali me ne sono convinto) ma per convincervi in maniera assoluta pensate allo stesso gioco però con 1000 scatole: il presentatore dopo la vostra scelta elimina 998 scatole assicurandovi che non ci sono premi in esse; a questo punto fareste lo scambio? io penso proprio di si: generalizzando questo gioco con N scatole, la probabilità di vincere dopo lo scambio è pari a (N-1)/N e quindi tende ad uno per il limite di scatole tendente ad infinito, ma a quel punto come potete scegliere fra un numero infinito di scatole?
P.S: il titolo del post è il nome dato a questo problema, per approfondimenti leggete wikipedia.
Posted: Dicembre 13th, 2008 | Author: packz | Filed under: Geometry, Hack, Letture, Life, Math | Commenti disabilitati su D.I.C.L.
Reduce da una festa di laurea il giovedì, giornata in cui si è osservato il fenomeno della dignità in caduta libera (D.I.C.L), ho ancora un mal di testa non indifferente; vomitare la mattina il kebab della sera prima è un sintomo di partecipazione e condivisione a cui non si sfugge ma che fa desiderare di non bere più (almeno a quei livelli). Se non ho subito danni irreparabili al mio cervello, prossimamente qualche trucco per far diventare ~NLogN l’algoritmo del pagerank…
Browser security handbook: direttamente da google un manuale relativo alla sicurezza nei browser; non l’ho letto tutto, ma pare interessante.
Graph theory: bel documentone PDF sulla teoria dei grafi.
Cool URIs don’t change: perché non cambiare gli URIs spiegato dal fondatore del web.
Anatomii of a hack: come fanno i people a caricare programmi propri nelle console? questo articolo fa un esempio pratico con un crack del Wii.
stackoverflow.com: sito molto interessante per tutti i tipi di sviluppatori: tu poni una questione e aspetti le risposte; alcune sono veramente interessanti.
Posted: Dicembre 8th, 2008 | Author: packz | Filed under: Math | 4 Comments »
Nell’aprile del 1998 due dottorandi americani della Stanford University pubblicano un articolo intitolato "the anatomy of a large-scale hypertextual web search engine" con cui descrivono un nuovo tipo di motore di ricerca con il quale riuscire a catalogare i contenuti del Web, usando i mezzi che le pagine ipertestuali stesse mettono a disposizione; il loro ambizioso progetto ha un nome che la dice lunga sull’ordine di grandezza della loro impresa: google, il modo comune di pronunciare googol, cioè il numero 100 elevato alla 100.
Read the rest of this entry »
Posted: Luglio 8th, 2008 | Author: packz | Filed under: Geometry, Life, Math, Physics | Commenti disabilitati su Flagelli
Posted: Luglio 8th, 2008 | Author: packz | Filed under: Geometry, Life, Math, Physics | Commenti disabilitati su La stagione dello studio

Posted: Aprile 9th, 2008 | Author: packz | Filed under: Math, Physics, Programmazione, TeX | Commenti disabilitati su Python e TeX
Le formule inserite nel post precedente sono state create attraverso il mio script per generare dei file png direttamente da codice TeX a linea di comando; come via è abbastanza comoda per ottenere delle formule da inserire nel blog, ma un passo successivo dovrebbe essere quello di inserire all’interno dell’interfaccia di gnome-blog un editor di equazioni. Prima di fare ciò però ho sviluppato un programma di python con il quale generare/visualizzare/salvare tramite una comoda interfaccia le formule composte in TeX.
Read the rest of this entry »
Posted: Aprile 7th, 2008 | Author: packz | Filed under: Geometry, Math, Physics | 1 Comment »
A volte la risposta è sempre stata lì, quasi come se l’avessi sempre saputa ma solo ad un certo punto ne sei consapevole; questo è successo alla mia persona per quanto riguarda il gruppo di Spin.
Partiamo dagli albori: nel 1922 il fisico Otto Stern e Walter Gerlach eseguirono un esperimento chiamato da quel giorno di Stern-gerlach (che fantasia poderosa) con cui misero fuori gioco la concezione meccanica classica per quanto riguarda le particelle elementari (già il trick di Planck per spiegare il paradosso della catastrofe ultravioletta aveva messo in dubbio il tutto, ma questo era un esperimento reale e senza possibili ri-interpretazioni); essi fecero passare degli atomi di argento per un campo magnetico disomogeneo facendoli impattare su una lastra fotografica per osservare così la loro distribuzione del momento angolare (detto spin). Un ragionamento classico ci avrebbe dovrebbe far credere che la distribuzione debba essere casuale, ma ciò non è: il momento angolare dell’ultimo elettrone che (spaiato) si trova nell’ultimo orbitale dell’argento, restituisce una volta misurato solo un risultato, o su o giù!!!
La cosa paradossale sta nel fatto che se mettiamo due macchine dell’esperimento in questione in serie, con il campo magnetico invariato, una particella con lo spin su rimarrà sempre con lo spin su… come se la misurazione fissasse la misura… ma questa è una storia che può portare troppo lontano…
Un bel giorno un giovane dal nome lungo e mirabolante decide di sorpassare le problematiche della meccanica quantistica standard per permetterle di passare la folle revisione della relatività introdotta da un impiegato dell’ufficio brevetti, cercando un operatore il cui quadrato fosse l’equazione di Klein-gordon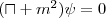 pensò alla seguente
pensò alla seguente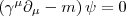 arrivando alla conclusione che gli elementi gamma avrebbero dovuto sottostare alla relazione
arrivando alla conclusione che gli elementi gamma avrebbero dovuto sottostare alla relazione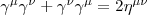 e che quindi quelle belle gamma dovevano essere per forza delle matrici; ottenne inoltre che le funzioni d’onda soluzioni di questa equazione incorporavano in automatico lo spin degli elettroni (in realtà questa equazione descrive qualunque fermione esista in natura) nonché le antiparticelle (dalla serie “la carta batte la camera a nebbia“).
e che quindi quelle belle gamma dovevano essere per forza delle matrici; ottenne inoltre che le funzioni d’onda soluzioni di questa equazione incorporavano in automatico lo spin degli elettroni (in realtà questa equazione descrive qualunque fermione esista in natura) nonché le antiparticelle (dalla serie “la carta batte la camera a nebbia“).
Il bello è che la relazione sopra mostrata ricalca quella con cui Clifford identifica quasi un secolo prima l’algebra che porta il suo nome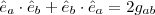 e che in pratica definisce una sorta di prodotto fra vettori in cui un vettore “moltiplicato” per se stesso genera un numero; può sembrare una definizione complessa ed inutile, ma si dà il caso che i numeri complessi, i quaternioni e gli ottonioni sono casi particolari di questa struttura matematica. Si può dimostrare che se prendiamo i prodotti pari di vettori unitari possiamo generare un gruppo, detto appunto di Spin, il quale agisce sui vettori complessi facendoli ruotare in una maniera particolare: una rotazione di 2 pi greco non riporta l’oggetto in questione nella posizione originale ma gli cambia segno! la rotazione identica risulta di ampiezza doppia ed è proprio il modo un cui si comportano gli elettroni.
e che in pratica definisce una sorta di prodotto fra vettori in cui un vettore “moltiplicato” per se stesso genera un numero; può sembrare una definizione complessa ed inutile, ma si dà il caso che i numeri complessi, i quaternioni e gli ottonioni sono casi particolari di questa struttura matematica. Si può dimostrare che se prendiamo i prodotti pari di vettori unitari possiamo generare un gruppo, detto appunto di Spin, il quale agisce sui vettori complessi facendoli ruotare in una maniera particolare: una rotazione di 2 pi greco non riporta l’oggetto in questione nella posizione originale ma gli cambia segno! la rotazione identica risulta di ampiezza doppia ed è proprio il modo un cui si comportano gli elettroni.
Qual’era la mia difficoltà? il non riuscire a trovare l’espressione degli elementi del gruppo di Spin e capire il perché, secondo la teoria topologica, questo gruppo ha due componenti connesse per metrica di segnature non banali (lettore capitato qui per caso non ti suicidare, quello che sto dicendo ha senso); ora io ho capito (qualunque cosa voglia dire)! prima di tutto siccome abbiamo detto che gli elementi del gruppo di Spin sono prodotti pari di vettori unitari, abbiamo che un elemento generico avrà la forma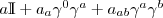 dove
dove e che quindi necessitiamo di 6 parametri per descrivere questo gruppo (nel caso in cui la metrica sia quella di Minkowski), ma per recuperare una forma meglio conosciuta ad un fisico possiamo definire le matrici
e che quindi necessitiamo di 6 parametri per descrivere questo gruppo (nel caso in cui la metrica sia quella di Minkowski), ma per recuperare una forma meglio conosciuta ad un fisico possiamo definire le matrici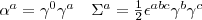 tramite cui descrivere un qualunque elemento di questo gruppo come prodotto di questi due
tramite cui descrivere un qualunque elemento di questo gruppo come prodotto di questi due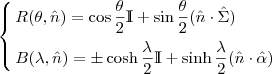 il primo rappresenta le rotazioni e il secondo i cambiamenti di velocità (detti boost) in pieno spirito relativistico. Da questa espressione risulta palese (???) che il gruppo è composto da due pezzi distinti, ognuno identificato dal segno davanti al coseno iperbolico (funzione che ha valori esclusivamente positivi e quindi non è possibile congiungere con una curva queste due varianti).
il primo rappresenta le rotazioni e il secondo i cambiamenti di velocità (detti boost) in pieno spirito relativistico. Da questa espressione risulta palese (???) che il gruppo è composto da due pezzi distinti, ognuno identificato dal segno davanti al coseno iperbolico (funzione che ha valori esclusivamente positivi e quindi non è possibile congiungere con una curva queste due varianti).
Spero che si capisca qualcosa in quello che ho scritto, se qualcuno si sente offeso dai miei sproloqui si faccia sentire…



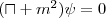 pensò alla seguente
pensò alla seguente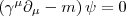 arrivando alla conclusione che gli elementi gamma avrebbero dovuto sottostare alla relazione
arrivando alla conclusione che gli elementi gamma avrebbero dovuto sottostare alla relazione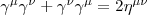 e che quindi quelle belle gamma dovevano essere per forza delle matrici; ottenne inoltre che le funzioni d’onda soluzioni di questa equazione incorporavano in automatico lo spin degli elettroni (in realtà questa equazione descrive qualunque fermione esista in natura) nonché le antiparticelle (dalla serie “la carta batte la
e che quindi quelle belle gamma dovevano essere per forza delle matrici; ottenne inoltre che le funzioni d’onda soluzioni di questa equazione incorporavano in automatico lo spin degli elettroni (in realtà questa equazione descrive qualunque fermione esista in natura) nonché le antiparticelle (dalla serie “la carta batte la 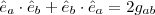 e che in pratica definisce una sorta di prodotto fra vettori in cui un vettore “moltiplicato” per se stesso genera un numero; può sembrare una definizione complessa ed inutile, ma si dà il caso che i numeri complessi, i
e che in pratica definisce una sorta di prodotto fra vettori in cui un vettore “moltiplicato” per se stesso genera un numero; può sembrare una definizione complessa ed inutile, ma si dà il caso che i numeri complessi, i 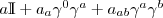 dove
dove e che quindi necessitiamo di 6 parametri per descrivere questo gruppo (nel caso in cui la metrica sia quella di Minkowski), ma per recuperare una forma meglio conosciuta ad un fisico possiamo definire le matrici
e che quindi necessitiamo di 6 parametri per descrivere questo gruppo (nel caso in cui la metrica sia quella di Minkowski), ma per recuperare una forma meglio conosciuta ad un fisico possiamo definire le matrici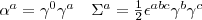 tramite cui descrivere un qualunque elemento di questo gruppo come prodotto di questi due
tramite cui descrivere un qualunque elemento di questo gruppo come prodotto di questi due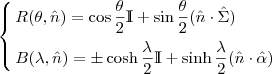 il primo rappresenta le rotazioni e il secondo i cambiamenti di velocità (detti
il primo rappresenta le rotazioni e il secondo i cambiamenti di velocità (detti 