L’algebra di Google
Posted: Dicembre 8th, 2008 | Author: packz | Filed under: Math | 4 Comments »
Nell’aprile del 1998 due dottorandi americani della Stanford University pubblicano un articolo intitolato "the anatomy of a large-scale hypertextual web search engine" con cui descrivono un nuovo tipo di motore di ricerca con il quale riuscire a catalogare i contenuti del Web, usando i mezzi che le pagine ipertestuali stesse mettono a disposizione; il loro ambizioso progetto ha un nome che la dice lunga sull’ordine di grandezza della loro impresa: google, il modo comune di pronunciare googol, cioè il numero 100 elevato alla 100.
La loro idea si basa sul fatto che le pagine, essendo per loro stessa natura ipertestuali, contengono dei cosiddetti (ma si scrive così, con 2 d?) link che puntano ad altre pagine probabilmente di argomento attinente con la stessa; inoltre le pagine con molti link che puntano ad essa sono anche molto importanti. Quindi si costruisce un valore detto PageRank (il termine Page viene dal suo inventore non è relativo al termine "pagina", sono proprio un coglione) costruito tramite la somma del Pagerank delle pagine che puntano ad essa, diviso per il numero totale di link totale per quella pagina. Guardate la seguente formula che esprime il concetto in maniera più fica
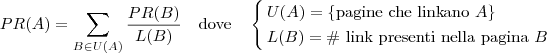

Quelli più furbi di voi avranno già subodorato lo sgamo: per calcolare il pagerank di una qualsiasi pagina, bisogna aver già calcolato il pagerank delle altre!!! Ma ecco che arriva la magia della matematica: è possibile definire una matrice H sifatta

grazie alla quale, se mettiamo tutti i valori del PageRank delle varie pagine come componenti di un vettore che chiamiamo I, la relazione precedente diventa


cioè una fottuta equazione agli autovalori!!! Prima di mostrarvi quali sono i problemi in tale visione, ecco un esempio pratico, con un web costituito da 8 pagine

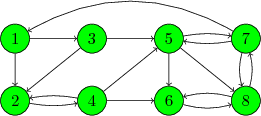
la sua matrice H è la seguente
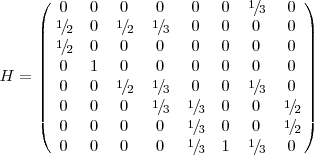
fico no? beh lo schifo è che il web ha qualche miliardino di pagine e le equazioni agli autovalori vengono di solito trovate come soluzione del polinomio caratteristico che ha grado pari alla dimensione della matrice: benché Abel sia morto povero, egli ci mostrò la via ed il fatto che polinomi con grado maggiore o uguale a 5 non hanno soluzione in forma chiusa. In realtà sono stati lui e Galois, entrambi abbastanza sfigati: uno morto povero benché avesse dimostrato un importante teorema ma pare che Cauchy perse il suo manoscritto e venne così pubblicato dopo la sua morte e l’altro morto in un duello a fuoco (pare la notte prima scrisse tutti i suoi risultati a imperitura memoria).
Tornando dal viaggio nel triste mondo dei matematici, il metodo, sempre matematico, è di usare il metodo delle potenze che permette di calcolare iterativamente l’autovettore tramite la relazione

La matrice H ha la proprietà che la somma delle sue colonne è sempre 1, il che la fa rientrare nel mondo delle matrici stocastiche e questo ci porta a una curiosa interpretazione di questo modello: prendiamo un web surfer che si muova attraverso i link della pagina, la matrice H ci dà la probabilità che da una pagina esso si muova verso un’altra ed è molto probabile che esso si ritrovi dopo un tempo sufficientemente lungo ad una pagina con un alto PageRank; questo risolve anche un problema: una pagina che non ha link, chiamata in questo modello un dangling node, si suca praticamente l’importanza delle pagine ad essa collegata senza restituire niente indietro. Dal punto di vista di un web surfer stocastico, arrivato a questa pagina, esso salterà con uguale probabilità ad una qualunque delle altre pagine del web, quindi al posto di avere la colonna di H con tutti 0, gli si mette una sfilza di 1/N dove N è il numero di pagine totali. Poi per finire si usa la matrice
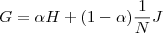
dove la matrice J è costituita da tutti 1, donando equiprobabilità per tutte le pagine; il termine alpha sceglie il comportamento del web-surfer-stocastico fra "seguitore di link" (alpha=1) oppure "viaggiatore random" (alpha=0). La cosa fica è che la velocità di convergenza del vettore dipende dal modulo di alpha e google lo ha scelto (pare) uguale a 0.85 (per 1 non converge ;-)).
Sicuro del fatto che non si capisce un cazzo, vi lascio qualche link
L’autovettore da 25.000.000$: qualche formula più formale.
Come google trova il tuo ago nel pagliaio del web: praticamente l’ho copiato da qui.
incominciamo ad alzare sto pagerank
rifondazione comunista nichelino http://prcnichelino.blog.tiscali.it//
Sono tentato di cancellare questo spudorato tentativo di marchetta… cmq google non si basa solo sul fakerank per tenere conto della pagina, ma anche, per esempio, ogni quanto viene aggiornata… anche sotto questo punto di vista quella pagina è veramente scarsa 😉
si, cosiddetti si scrive con due d
Molto interessante! grazie Packs di queste chicche…tra l’altro ho una risposta in più quando a ripetezioni mi chiederanno “ma a che cacchio serve le geometria?” :D:D
Pino