Teoria dell’informazione
Posted: Settembre 20th, 2007 | Author: packz | Filed under: Physics | 4 Comments »Dopo una serata a bere come un pazzo ed alzarmi con la cavità orale somigliante a livello organolettico ad una fogna di calcutta, mi appresto a scrivere un bel post per spiegare finalmente che cazzo significa la frase scritta nella testata del blog: bisogna partire da un pochino lontano, probabilmente con la frase "c'era una volta".Con la pubblicazione nel 1948 di "A mathematical theory of communication" da parte di C. E. Shannon, cambia il modo di intendere il concetto l'informazione, rendendo tutto quello che ci sta alla base una scienza esatta; più che altro il nostro amato scienziato riesce a definire cosa si intende per essa a livello matematico.
Non so se lo sapete, ma nel codice morse il punto rappresenta la lettera più frequente nei testi inglesi, cioé la lettera "e", questo permette di risparmiare tempo e fatica nella digitazione: bene questa è una delle cosa che possono iniziare a far comprendere lo scopo dei lavori di Shannon, cioé che le lettere e anche le parole hanno una correlazione tra loro (in italiano se una parola inizia con la "Q" siamo certi che la prossima lettera sarà una "U"). Quello che si poneva come obiettivo era rispondere alla questione
Supponiamo di avere una sorgente che produca messaggi di un dato tipo (come per esempio in italiano). Supponiamo di avere un canale di comunicazione disturbato e con determinate caratteristiche. In che modo possiamo rappresentare o codificare messaggi della sorgente mediante segnali elettrici, così da ottenere la più rapida trasmissione possibile nel canale disturbato? Equivalentemente: con quale rapidità si può trasmettere senza errore un dato tipo di messaggio in un certo canale?
Senza entrare nei dettagli che potete trovare nel testo originale o in libri appositi, Shannon definì tramite la formula
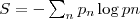
una grandezza definita entropia che rappresenta la quantità di informazione (in bit siccome viene usato il logaritmo di 2) insita nel messaggio (p_n rappresentano le probabilità degli n simboli che è possibile incontrare nel messaggio): volendo fare degli esempi banali, se la sorgente sputasse fuori solo il valore 0 allora avremmo p_n pari ad 1 (si ha certezza) e guarda caso il log di 1 è zero, non ho informazione da questo messaggio; nel caso di un lancio di una moneta ho due evento equiprobabili (p_n = 1/2) e quindi
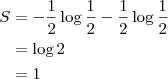
si ottiene che devo usare 1 bit di informazione ad ogni lancio per sapere se è uscito testa oppure croce. Ovviamente per il linguaggio la situazione è più complicata siccome esiste una correlazione a più livelli fra le singole lettere e le parole (la lingua inglese ha una entropia compresa fra 0.6 e 1.3 bit per lettera). Comunque l'entropia restituisce la "dimensione" dei messaggi probabili proporzionale a 2 elevato al valore dell'entropia (tornando all'esempio della Q, è impossibile trovare parole come "qano" in un messaggio in italiano corretto).
Durante i suoi studi è arrivato a dedurre che in un un canale con ampiezza di banda W, su cui si trasmette con una potenza P, ma con un rumore dato da N, si ha una trasmissione di C bit al secondo data dalla formula
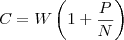
d'altronde nel caso di rumore termico totalmente casuale si ha
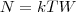
Sostituendo in C quest'ultima relazione e passando al limite per una banda molto grande (matematucamente si fa il limite per W che tende ad infinito) ed infine ribaltando la relazione rispetto alla potenza di trasmissione, si ottiene
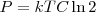
che in pratica ci dice che per ogni bit trasmesso bisogna "spendere" almeno kTln2 joules di energia per trasmettere un messaggio in un ambiente a temperatura T.
Voi penserete: "bella, ma chi se ne frega!!! è più interessante il teorema di incompletezza di Goedel" ma io che sono fisico vi dico che questa deduzione è importantissima! prima di tutto la deduzione è fatta senza entrare del merito del tipo di canale sia (telepatia, rete WiFi, amore) secondo, il fatto che la grandezza introdotta da Shannon si chiami entropia non vi fa scattare un allarme? no, non èil pacemaker…
Qualcuno di voi saprà sicuramente che il secondo principio della termodinamica proibisce di costruire macchine che possano trasformare completamente in lavoro il calore fornitogli e che questo è equivalente all'impossibilità di far passare il calore da un corpo freddo ad uno caldo come unica trasformazione: Maxwell aveva inventato un paradosso secondo il quale, se fosse esistito un essere abbastanza piccolo da poter vedere le singole particelle di un gas e fosse rinchiuso in una scatola in cui fossero stati preseni due gas a temperature diverse separati da una parete divisoria, questo demoniaccio avrebbe potuto osservare le particelle più veloci e tramite uno sportello fa passare queste nella parte più fredda (in cui le particelle si muovono più lentamente) permettendo al calore di passare da un corpo freddo ad uno caldo senza colpo ferire! Adesso che però siamo a conoscenza degli studi di Shannon, sappiamo che il nostro diavoletto individuare la posizione delle particelle e la loro direzione con accuratezza per farle passare attraverso il pertugio e per fare questo ha bisogno di informazioni che gli saranno donate in cambio di energia… se si fanno i conti esattamente si scopre che l'energia che guadagna il box è esattamente quella spesa dal diavoletto…
Per approfondimenti il mio seminario…
P.S: Ho scritto il tutto un po' di fretta, mi scuso per gli errori e la mia incapacità di scrivere…
innanzitutto “finalmente trovo su noblogs qualcuno che scrive su ste cose”.
comunque la confutazione del diavoletto di maxwell è arrivata 50 anni prima di shannon, da ludwig boltzmann, tanto che successivamente al diavoletto di maxwell è venuto anche il diavoletto di loschmidt che era quello che diminuiva l’entropia invertendo le velocità delle molecole dopo gli urti. boltzmann disse a loschmidt “prego, le inverta lei”.
in realtà entrambi i processi accadono, e ce lo dice la meccanica statistica, solo che se per un paio di molecole che causano una diminuzione di entropia 10^20 la aumentano non è un grande risultato.
sei fisico anche tu ? che anno e dove ?
altra cosa: che layout è quello di latex che hai usato nel pdf ? è abbastanza figo e “moderno”, mi piacerebbe rubartelo. se non l’hai già letto, ti consiglio “il programma dell’universo” di seth lloyd ( te lo dice uno che non legge praticamente un cazzo ), ha una bella fila di digressioni storiche e discussioni di questo tipo.
Beh anche il tuo blog non è niente male…
Quello che uso per scrivere i documenti è il TeX e non LaTeX e le macro le ho scritte personalmente; in effetti dovrei mettere le macro online (ed in particolare il sorgente di quel documento) ma non ho tempo di pulire la merda nel codice…
Io sono già laureato in Fisica ma sto facendo il dottorato a Matematica: purtroppo sono entrato nel lato oscuro della programmazione in questo periodo.
Per il libro vedrò di procurarmelo.
ah io non mi sono mai cimentato in scrivere le macro, quando avrò voglia magari !
comunque le robe sui diavoletti sono ben illustrate in quel libro, fra termodinamica e teoria dell’informazione, fa al caso tuo, l’autore è uno dei grossi nella costruzione di computer quantistici.